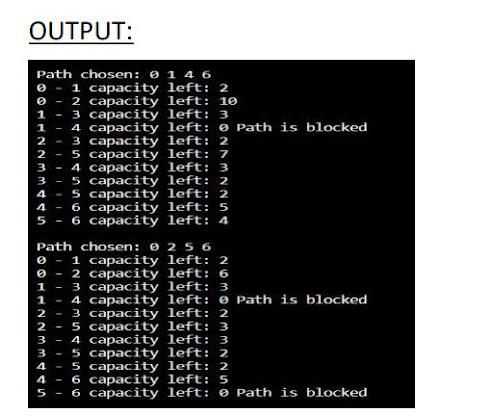
FORD-FULKERSON maximum flow ALGORITHM with User Input
#include <stdio.h>
#define A 0
#define B 1
#define C 2
#define MAX_NODES 1000
#define O 1000000000
int n;
int e;
int capacity[MAX_NODES][MAX_NODES];
int flow[MAX_NODES][MAX_NODES];
int color[MAX_NODES];
int pred[MAX_NODES];
int min(int x, int y) {
return x < y ? x : y;
}
int head, tail,top;
int q[MAX_NODES + 2];
int path[MAX_NODES];
void enqueue(int x) {
q[tail] = x;
tail++;
color[x] = B;
}
int dequeue() {
int x = q[head];
head++;
color[x] = C;
return x;
}
void push(int x){
path[top]=x;
top++;
}
int pop(){
int output = path[top];
top--;
return output;
}
// Using BFS as a searching algorithm
int bfs(int start, int target) {
int u, v;
for (u = 0; u < n; u++) {
color[u] = A;
}
head = tail = 0;
enqueue(start);
pred[start] = -1;
while (head != tail) {
u = dequeue();
for (v = 0; v < n; v++) {
if (color[v] == A && capacity[u][v] - flow[u][v] > 0) {
enqueue(v);
pred[v] = u;
}
}
}
return color[target] == C;
}
void residual_graph(){
int i,j;
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(capacity[i][j]!=0){
printf("\n%d - %d capacity left: %d",i,j,capacity[i][j]-
flow[i][j]);
if((capacity[i][j]-flow[i][j])==0)
printf(" Path is blocked");
}
}
}
}
// Applying fordfulkerson algorithm
int fordFulkerson(int source, int sink) {
int i, j, u;
int max_flow = 0;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
flow[i][j] = 0;
}
}
// Updating the residual values of edges
while (bfs(source, sink)) {
int increment = O;
for (u = n - 1; pred[u] >= 0; u = pred[u]) {
increment = min(increment, capacity[pred[u]][u] -
flow[pred[u]][u]);
}
top=0;
for (u = n - 1; pred[u] >= 0; u = pred[u]) {
push(u);
flow[pred[u]][u] += increment;
flow[u][pred[u]] -= increment;
}
push(u);
// Adding the path flows
max_flow += increment;
printf("\nPath chosen: ");
pop();
while(top>=0){
printf("%d ",pop());
}
residual_graph();
printf("\n");
}
return max_flow;
}
int main() {
int start,end,c,source,sink,i,j;
printf("Enter number of vertices: \n");
scanf("%d",&n);
printf("Enter number of edges: \n");
scanf("%d",&e);
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
capacity[i][j] = 0;
}
}
//int i;
for(i=1;i<=e;i++){
printf("Enter start vertex,end vertex and capacity for edge %d\n",i);
scanf("%d%d%d",&start,&end,&c);
capacity[start][end] = c;
}
printf("\n Enter source and sink vertices\n");
scanf("%d%d",&source,&sink);
printf("Max Flow: %d\n", fordFulkerson(source, sink));
}